This is part 1 of a multi-part post about rocket nozzles.

I have been kicking around some rocket nozzle ideas for a while now, and now that I have a 3d printer, I actually have fabrication capabilities at my disposal. Granted, plastic filament is not a very practical material for rocket nozzles, however I have never practicality get in the way of good fun.

I was going to wait a while before posting my work, but I see people collaborating online at github/thingiverse/reprap forums working on a similar project, so I figured I’d draw a line in the sand and share what I’ve got so far.

In part 1, I will lay out the sketches of the nozzle that I set out to build — a de Laval converging-diverging nozzle using G.V. Rao’s geometry — and develop the equations that describe such a nozzle.

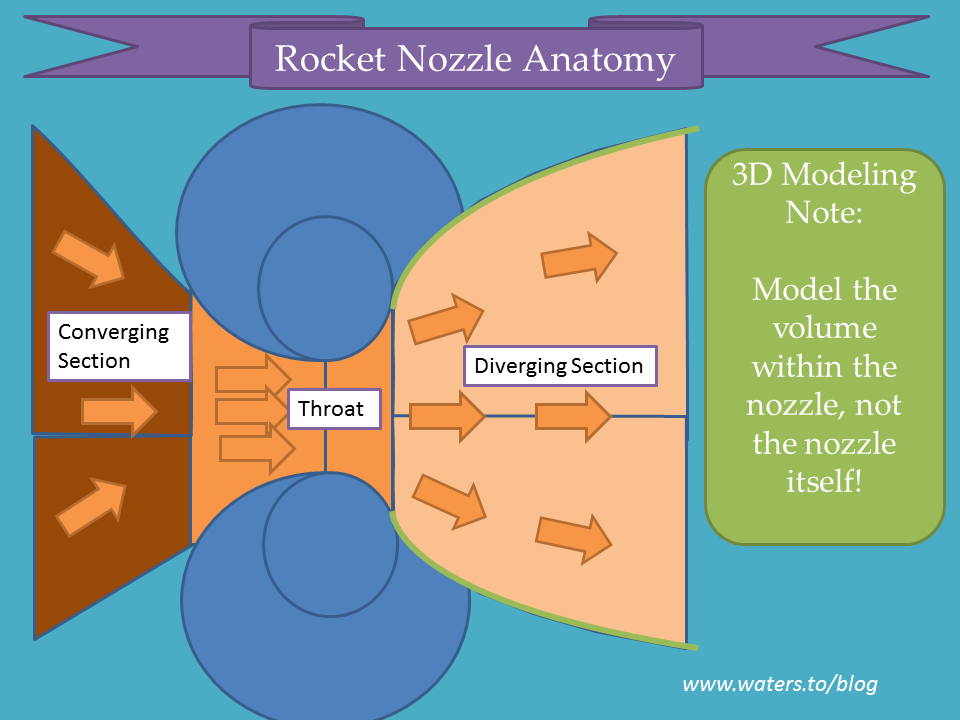
The idea behind a converging-diverging nozzle is that exhaust gases will accelerate through the converging cone, reaching mach 1 — the speed of sound — as they pass through the throat. Once past the constriction, the gases will expand and further accelerate and become supersonic. The final velocity reached depends on gas thermodynamics and the exact geometry of the nozzle, but today’s rockets routinely achieve exhaust velocities of several times the speed of sound.

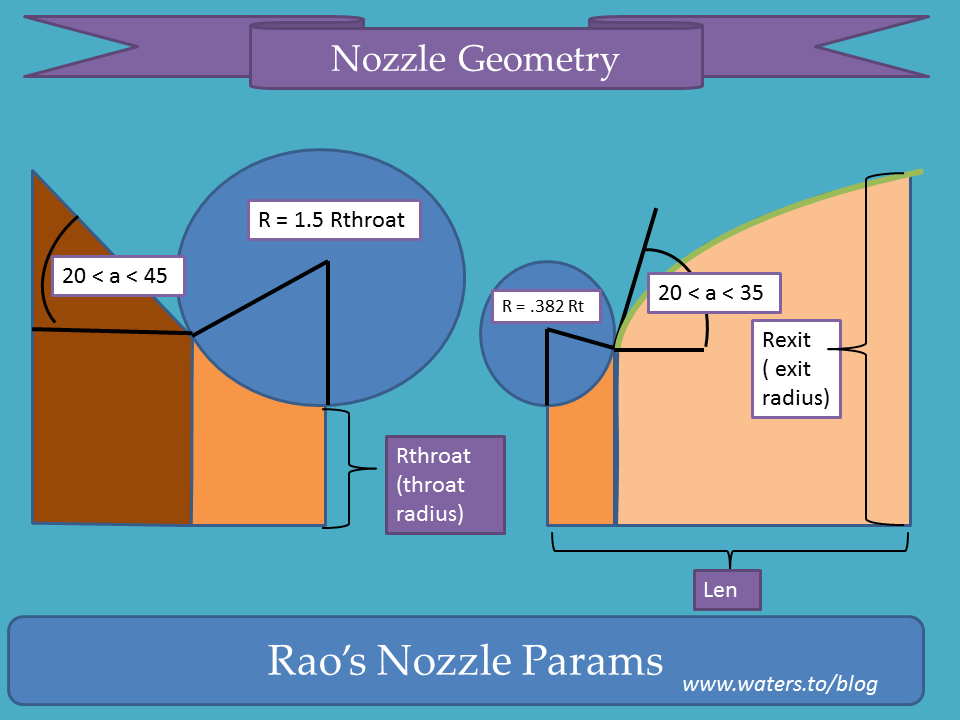
The geometry underlying the nozzle is fairly simple — a cone, two arcs, and a parabola, as described by G.V. Rao in 1958. See section 2.4.1 and 2.4.2 for some excellent bedtime reading about Dr. Rao’s results: http://www.scribd.com/doc/58809639/13/Bell%C2%A0nozzle

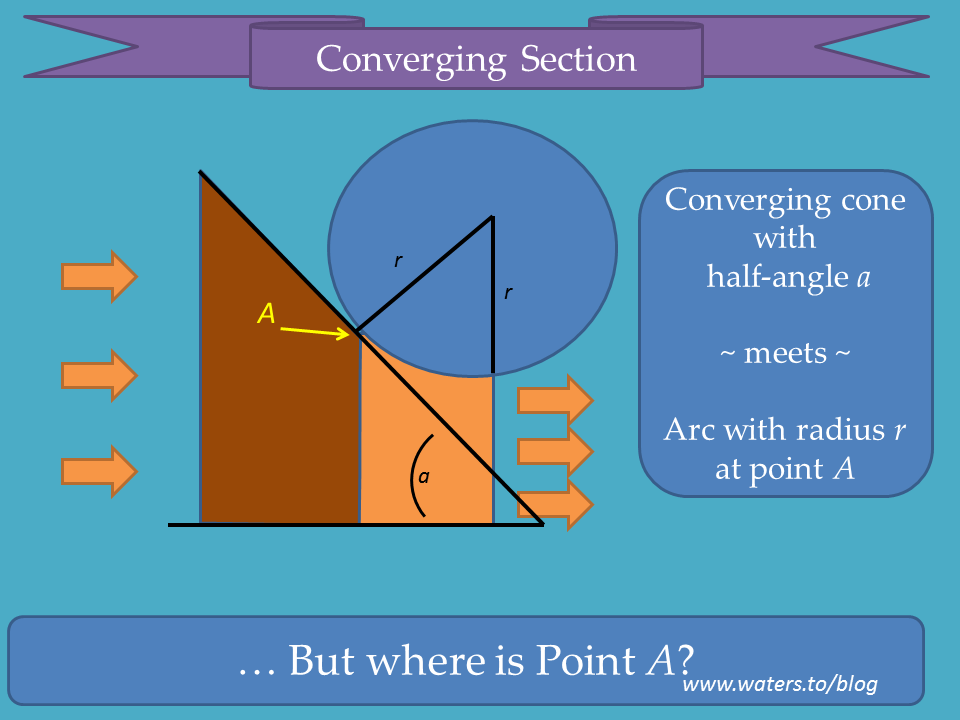
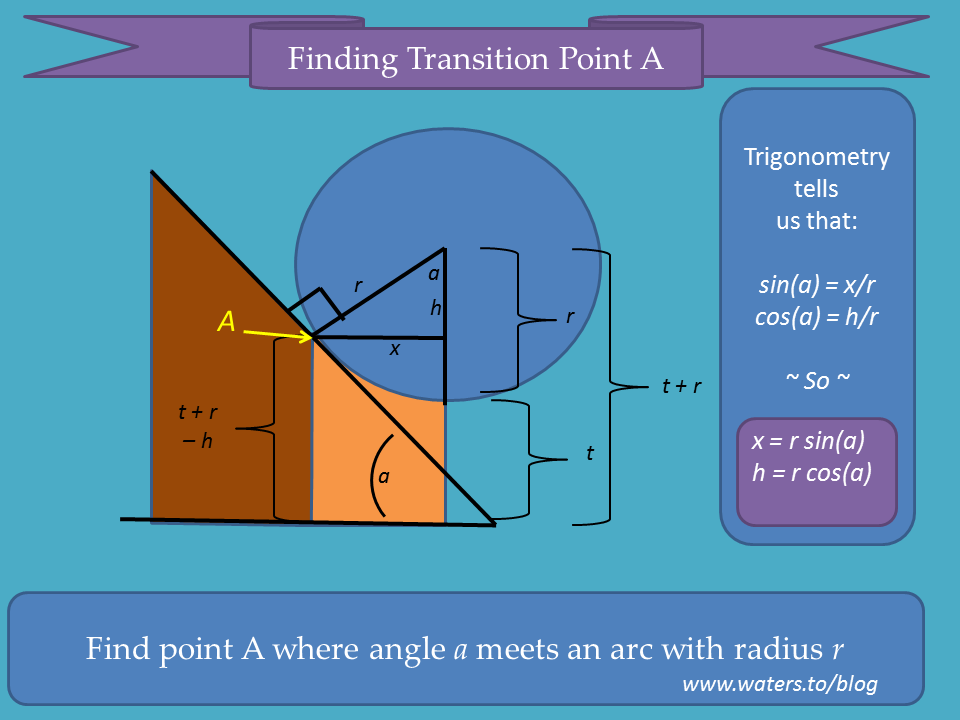
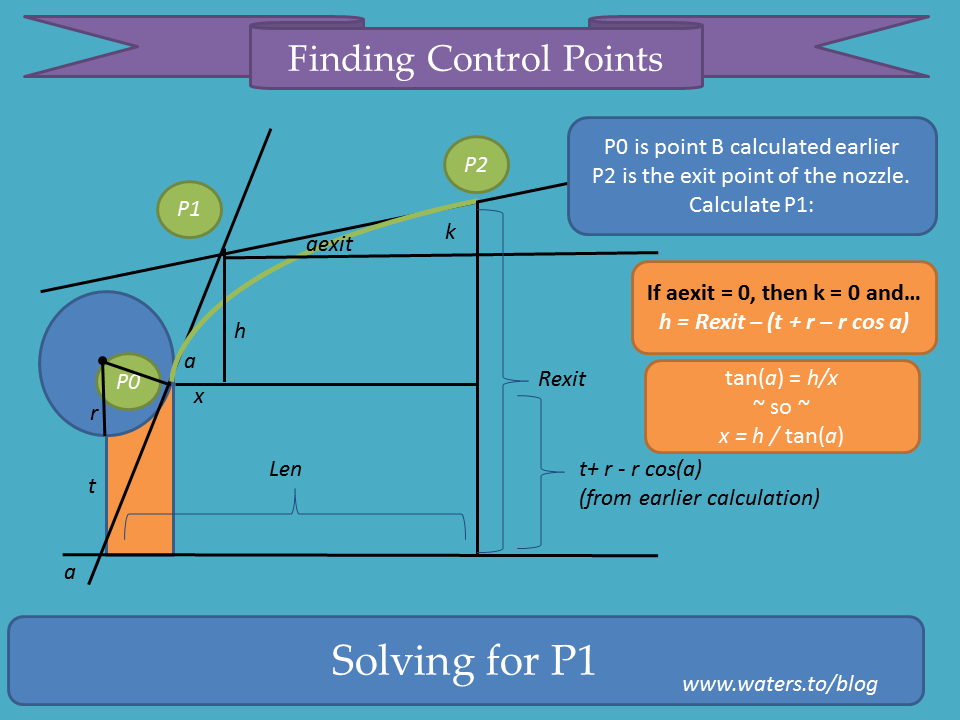
In order to model this nozzle in OpenSCAD, I first needed to determine up a few key points mathematically, so I threw together a more detailed sketch suitable for reasoning about the trig:

Here it is again, with the details worked out for the cone-to-throat transition:

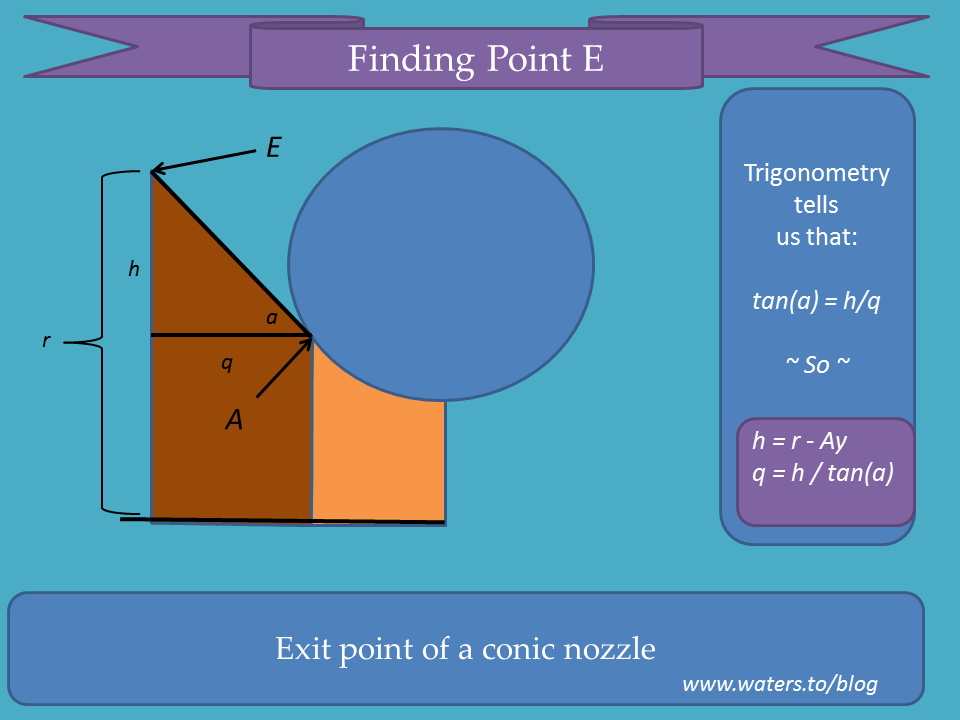
And here are the details for the inlet cone itself:

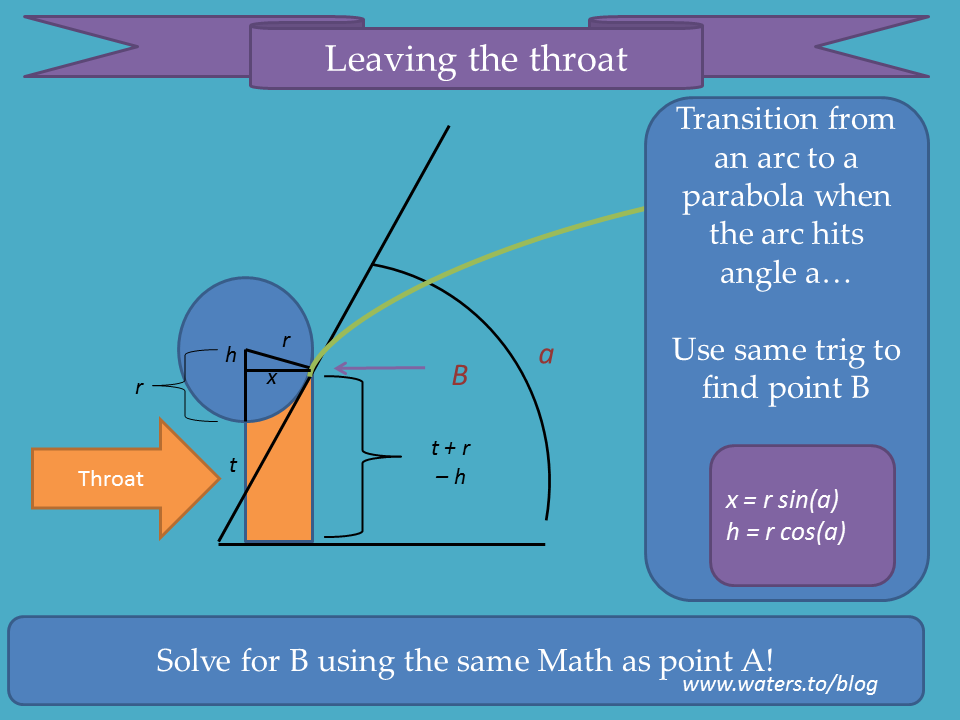
The arc transitioning out of the throat is set up the same as the arc in, just with a different radius.

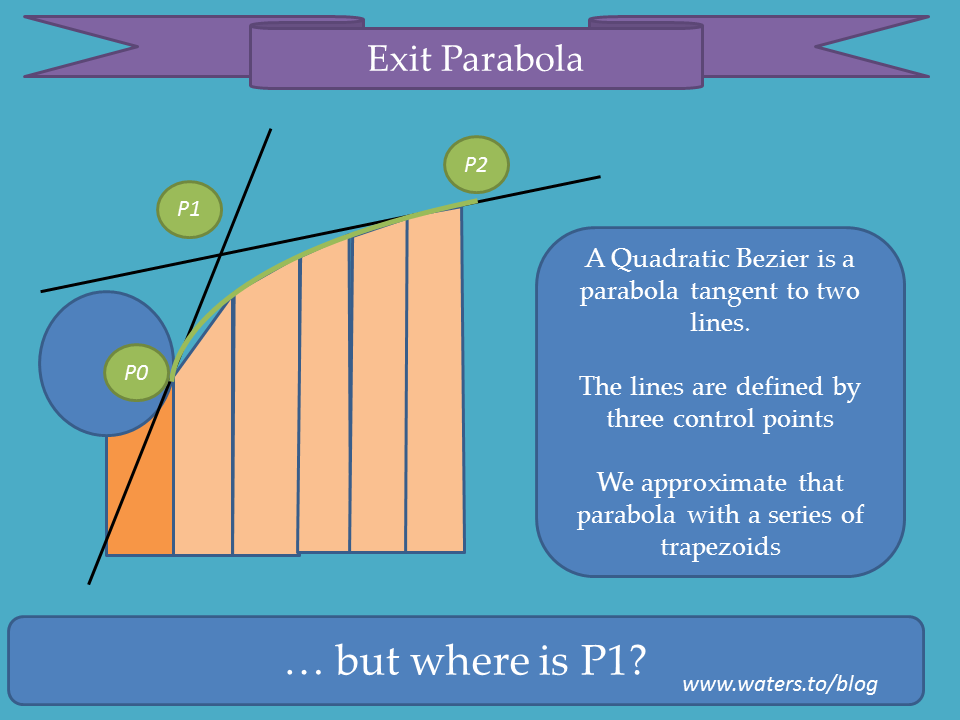
The arc out of the throat needs to join smoothly with the parabolic expansion section. Mathematically, that means that both the arc and parabola are tangent to the same line at the transition point. I admit, I was stuck here until I saw github user buback note that a quadratic bezier curve forms a nice parabola. I adapted the algorithm he found to use a trapezoidal approximation of the curve.

The last bit of math is to find point P1…

And that’s it! If you followed this far, you paid attention in High School Trigonometry! Wish you paid more attention? Khan Academy has great free tutorials!

In Part 2 I will use all of this math to design an OpenSCAD script to build 2d and 3d models of the nozzle!